Teknokiper.com - Teorema atau dalil phytagoras adalah suatu teori yang menunjukkan hubungan antara sisi-sisi dalam sebuah segitiga siku-siku. Dalil pythagoras merupakan salah satu topik penting dalam bidang study matematika dan diaplikasikan pada bidang ilmu lainnya seperti fisika, astronomi, arsitektur, dan sebagainya. Tak hanya digunakan dalam perhitungan bidang dua dimensi, teorema pythagoras juga sering digunakan dalam perhitungan bangun toga dimensi. Sesuai dengan namanya, teorema pytaghoras pertama kali ditemukan oleh seorang ahli matematika berkebangsaan Yunani bernama Pythagoras. Dengan menggunakan dali pythagoras, kita dapat menentukan panjang salah satu sisi segitiga siku-siku jika panjang dua sisi lainnya diketahui. Lalu, bagaimana hubungan antara sisi-sisi dalam segitiga siku-siku? Pada kesempatan ini, teknokiper akan membahas rumus teorema pythagoras dan kegunaannya.
Sebelum kita membahas teorema pythagoras dan kegunaannya, ada baiknya kita mengenal apa itu segitiga siku-siku. Segitiga adalah bangun datar yang memiliki tiga sisi dan tiga sudut. Segitiga siku-siku adalah segitiga yang salah satu sudutnya bernilai 90o.
Sebuah segitiga biasanya dinamai berdasarkan nama dari ketiga sudutnya. Misalnya, segitiga ABC mempunyai tiGa sudut yaitu sudut A, sudut B, dan sudut C. Selain itu, sisi yang berada di depan sudut juga diberi nama sesuai dengan nama sudutnya tapi menggunakan huruf kecil.
Sebagai contoh, pada segitiga siku-siku ABC, sisi di hadapan sudut sudut A dinamakan sisi a, sisi yang berada di hadapan sudut B dinamakan sisi b, dan sisi yang berada di hadapan sudut C dinamakan sisi c.
Untuk lebih jelasnya, perhatikan gambar berikut!
Keterangan :
Sisi a = garis BC, sisi di depan sudut A
Sisi b = garis AC, sisi di depan sudut B
Sisi c = garis AB, sisi di depan sudut C
Selain dinamakan sesuai dengan nama sudut di hadapannya, sisi-sisi pada segitiga siku-siku juga bisa dinamakan berdasarkan posisi sikunya, yaitu:
1. Sisi miring = sisi terpanjang, sisi di hadapan sudut siku
2. Sisi penyiku = dua sisi yang mengapit siku-siku
Pada gambara segitiga siku-siku ABC di atas, sisi a merupakan sisi miring dan sisi terpanjang dalam segitiga itu. Sedangkan sisi b dan sisi c merupakan sisi penyiku.
Baca juga : Mengubah Bentuk Pecahan ke Bentuk Lain.
Sesuai dengan teorema tersebut, maka hubungan sisi-sisi dalam segitiga siku-siku dapat ditulis sebagai berikut:
Keterangan :
BC = terpanjang
AC dan AB = sisi penyiku
Contoh Soal:
Sebuah segitiga ABC siku-siku di A dengan panjang AB = 3 cm. Jika panjang sisi terpanjangnya adalah 5 cm, maka tentukanlah panjang sisi lainnya.
Pembahasan :
Dik : AB = c = 3 cm, BC = a = 5 cm
Dit : b = ... ?
Berdasarkan teorema Pythagoras:
⇒ a2 = b2 + c2
⇒ 52 = b2 + 32
⇒ 25 = b2 + 9
⇒ b2 = 25 - 9
⇒ b2 = 16
⇒ b = √16
⇒ b = 4
Jadi, sisi lainnya adalah 4 cm.
1. Menentukan panjang diagonal persegi
2. Menentukan diagonal ruang kubus dan balok
#1 Panjang Diagonal persegi
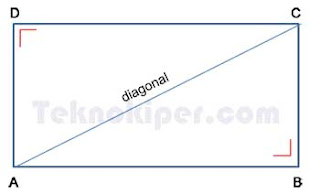
Diberikan sebuah persegi panjang ABCD seperti terlihat pada gambar di bawah ini.
Garis AC adalah garis diagonal persegi. Jika panjang sisi-sisi persegi tersebut diketahui, maka panjang diagonalnya dapat dihitung dengan memanfaatkan dalil Pythagoras:
Contoh Soal :
Sebuah persegi ABCD memiliki panjang 8 cm dan lebar 6 cm. Tentukanlah panjang diagonal persegi tersebut.
Pembahasan :
Dik : panjang = p = 8 cm, lebar = L = 6 cm
Dit : diagonal = d = ... ?
Berdasarkan dalil Pythagoras:
⇒ d2 = p2 + L2
⇒ d2 = 82 + 62
⇒ d2 = 64 + 36
⇒ d2 = 100
⇒ d = √100
⇒ d = 10 cm
Jadi, panjang diagonal persegi itu adalah 10 cm.
Baca juga : Soal dan Pembahasan Unsur-unsur Lingkaran.
#2 Panjang Diagonal ruang
Diberikan sebuah balok ABCD.EFGH seperti terlihat pada gambar di bawah ini.
Garis AG adalah salah satu diagonal ruang dalam balok tersebut. Panjang diagonal ruang AG dapat dihitung berdasarkan dalil Pythagoras sebagai berikut:
Keterangan :
AG = diagonal ruang
CG = tinggi balok
AC = diagonal bidang alas
Selanjutnya perhatikan alas balok yaitu persegi ABCD. Berdasarkan dali Pythagoras, panjang diagonal bidang AC dapat dihitung dengan rumus berikut:
Keterangan :
AB = panjang balok
BC = lebar balok
Karena AC2 = AB2 + BC2, maka rumus panjang diagonal ruang AG dapat diubah menjadi:
⇒ AG2 = AC2 + CG2
⇒ AG2 = AB2 + BC2 + CG2
⇒ AG2 = p2 + L2 + t2
Maka rumusnya menjadi:
Keterangan :
dr = diagonal ruang
p = panjang balok
L = lebar balok
t = tinggi balok
Contoh Soal :
Sebuah balok mempunyai panjang, lebar, dan tinggi berturut-turut adalah 12 cm, 9 cm, dan 8 cm. Tentukanlah panjang salah satu diagonal ruangnya.
Pembahasan :
Dik : p = 12 cm, L = 9 cm, dan t = 8cm
Dit : dr = ... ?
Berdasarkan dalil Pythagoras:
⇒ dr2 = p2 + L2 + t2
⇒ dr2 = 122 + 9sup>2 + 82
⇒ dr2 = 144 + 81 + 64
⇒ dr2 = 289
⇒ dr = √289
⇒ dr = 17 cm
Jadi, panjang diagonal ruangnya adalah 17 cm.
Baca juga : Kumpulan Soal dan Pembahasan Teorema Pythagoras.
Sebelum kita membahas teorema pythagoras dan kegunaannya, ada baiknya kita mengenal apa itu segitiga siku-siku. Segitiga adalah bangun datar yang memiliki tiga sisi dan tiga sudut. Segitiga siku-siku adalah segitiga yang salah satu sudutnya bernilai 90o.
Sebuah segitiga biasanya dinamai berdasarkan nama dari ketiga sudutnya. Misalnya, segitiga ABC mempunyai tiGa sudut yaitu sudut A, sudut B, dan sudut C. Selain itu, sisi yang berada di depan sudut juga diberi nama sesuai dengan nama sudutnya tapi menggunakan huruf kecil.
Sebagai contoh, pada segitiga siku-siku ABC, sisi di hadapan sudut sudut A dinamakan sisi a, sisi yang berada di hadapan sudut B dinamakan sisi b, dan sisi yang berada di hadapan sudut C dinamakan sisi c.
Untuk lebih jelasnya, perhatikan gambar berikut!
Keterangan :
Sisi a = garis BC, sisi di depan sudut A
Sisi b = garis AC, sisi di depan sudut B
Sisi c = garis AB, sisi di depan sudut C
Selain dinamakan sesuai dengan nama sudut di hadapannya, sisi-sisi pada segitiga siku-siku juga bisa dinamakan berdasarkan posisi sikunya, yaitu:
1. Sisi miring = sisi terpanjang, sisi di hadapan sudut siku
2. Sisi penyiku = dua sisi yang mengapit siku-siku
Pada gambara segitiga siku-siku ABC di atas, sisi a merupakan sisi miring dan sisi terpanjang dalam segitiga itu. Sedangkan sisi b dan sisi c merupakan sisi penyiku.
Baca juga : Mengubah Bentuk Pecahan ke Bentuk Lain.
Bunyi dan Rumus Dalil Pythagoras
Teorema Pythagoras menjelaskan hubungan antara panjang sisi-sisi pada segitiga siku-siku. Bunyi teorema Pythagoras adalah "Pada segitiga siku-siku, kuadrat sisi terpanjang adalah sama dengan jumlah kuadrat sisi-sisi penyikunya".Sesuai dengan teorema tersebut, maka hubungan sisi-sisi dalam segitiga siku-siku dapat ditulis sebagai berikut:
| BC2 = AC2 + AB2 |
| a2 = b2 + c2 |
Keterangan :
BC = terpanjang
AC dan AB = sisi penyiku
Contoh Soal:
Sebuah segitiga ABC siku-siku di A dengan panjang AB = 3 cm. Jika panjang sisi terpanjangnya adalah 5 cm, maka tentukanlah panjang sisi lainnya.
Pembahasan :
Dik : AB = c = 3 cm, BC = a = 5 cm
Dit : b = ... ?
Berdasarkan teorema Pythagoras:
⇒ a2 = b2 + c2
⇒ 52 = b2 + 32
⇒ 25 = b2 + 9
⇒ b2 = 25 - 9
⇒ b2 = 16
⇒ b = √16
⇒ b = 4
Jadi, sisi lainnya adalah 4 cm.
Kegunaan Dalil Pythagoras
Selain digunakan untuk menentukan panjang salah satu sisi segitiga yang tidak diketahui, dali Pythagoras juga dapat digunakan pada beberapa perhitungan, antaralain:1. Menentukan panjang diagonal persegi
2. Menentukan diagonal ruang kubus dan balok
#1 Panjang Diagonal persegi
Diberikan sebuah persegi panjang ABCD seperti terlihat pada gambar di bawah ini.
Garis AC adalah garis diagonal persegi. Jika panjang sisi-sisi persegi tersebut diketahui, maka panjang diagonalnya dapat dihitung dengan memanfaatkan dalil Pythagoras:
| AC2 = AB2 + BC2 |
| AC2 = AD2 + CD2 |
Contoh Soal :
Sebuah persegi ABCD memiliki panjang 8 cm dan lebar 6 cm. Tentukanlah panjang diagonal persegi tersebut.
Pembahasan :
Dik : panjang = p = 8 cm, lebar = L = 6 cm
Dit : diagonal = d = ... ?
Berdasarkan dalil Pythagoras:
⇒ d2 = p2 + L2
⇒ d2 = 82 + 62
⇒ d2 = 64 + 36
⇒ d2 = 100
⇒ d = √100
⇒ d = 10 cm
Jadi, panjang diagonal persegi itu adalah 10 cm.
Baca juga : Soal dan Pembahasan Unsur-unsur Lingkaran.
#2 Panjang Diagonal ruang
Diberikan sebuah balok ABCD.EFGH seperti terlihat pada gambar di bawah ini.
Garis AG adalah salah satu diagonal ruang dalam balok tersebut. Panjang diagonal ruang AG dapat dihitung berdasarkan dalil Pythagoras sebagai berikut:
| AG2 = AC2 + CG2 |
Keterangan :
AG = diagonal ruang
CG = tinggi balok
AC = diagonal bidang alas
Selanjutnya perhatikan alas balok yaitu persegi ABCD. Berdasarkan dali Pythagoras, panjang diagonal bidang AC dapat dihitung dengan rumus berikut:
| AC2 = AB2 + BC2 |
Keterangan :
AB = panjang balok
BC = lebar balok
Karena AC2 = AB2 + BC2, maka rumus panjang diagonal ruang AG dapat diubah menjadi:
⇒ AG2 = AC2 + CG2
⇒ AG2 = AB2 + BC2 + CG2
⇒ AG2 = p2 + L2 + t2
Maka rumusnya menjadi:
| dr2 = p2 + L2 + t2 |
Keterangan :
dr = diagonal ruang
p = panjang balok
L = lebar balok
t = tinggi balok
Contoh Soal :
Sebuah balok mempunyai panjang, lebar, dan tinggi berturut-turut adalah 12 cm, 9 cm, dan 8 cm. Tentukanlah panjang salah satu diagonal ruangnya.
Pembahasan :
Dik : p = 12 cm, L = 9 cm, dan t = 8cm
Dit : dr = ... ?
Berdasarkan dalil Pythagoras:
⇒ dr2 = p2 + L2 + t2
⇒ dr2 = 122 + 9sup>2 + 82
⇒ dr2 = 144 + 81 + 64
⇒ dr2 = 289
⇒ dr = √289
⇒ dr = 17 cm
Jadi, panjang diagonal ruangnya adalah 17 cm.
Baca juga : Kumpulan Soal dan Pembahasan Teorema Pythagoras.


0 comments :
Post a Comment